Rozkład t-Studenta to ważne narzędzie statystyczne, które można łatwo obliczyć w programie Excel. Kluczowa funkcja to ROZKŁAD.T, która pozwala na szybkie obliczenia prawdopodobieństwa dla różnych wartości t. Wymaga ona trzech argumentów: wartości x, stopni swobody i typu rozkładu (jedno- lub dwustronny). Excel oferuje też nowsze, dokładniejsze funkcje jak ROZKŁAD.T.RT i ROZKŁAD.T.2T.
Najważniejsze informacje:- Funkcja ROZKŁAD.T ma składnię: =ROZKŁAD.T(x; stopnie_swobody; strony)
- Można wybrać rozkład jednostronny (1) lub dwustronny (2)
- Stopnie swobody muszą być ≥ 1
- Dla ujemnych wartości x istnieją specjalne relacje
- Nowsze funkcje (ROZKŁAD.T.RT, ROZKŁAD.T.2T) są zalecane do użycia
Co to jest rozkład t-Studenta?
Rozkład t-Studenta to kluczowe narzędzie statystyczne, wykorzystywane głównie w sytuacjach, gdy mamy do czynienia z małymi próbami. Służy do estymacji średniej populacji, gdy odchylenie standardowe tej populacji jest nieznane. Jest szczególnie przydatny w badaniach naukowych, analizach ekonomicznych i kontroli jakości.
Jego zastosowanie jest nieocenione w testowaniu hipotez statystycznych, zwłaszcza gdy wielkość próby jest ograniczona. Rozkład t-Studenta pozwala na precyzyjne wnioskowanie o parametrach populacji, nawet gdy dysponujemy niewielką ilością danych, co czyni go niezastąpionym w wielu dziedzinach nauki i biznesu.
- Masz małą próbę (n < 30)
- Nie znasz odchylenia standardowego populacji
- Chcesz porównać średnie dwóch grup lub sprawdzić, czy średnia próby różni się istotnie od hipotetycznej wartości populacji
Funkcja ROZKŁAD.T w Excelu - podstawy
Excel oferuje wbudowaną funkcję ROZKŁAD.T, która umożliwia szybkie i precyzyjne obliczenia związane z rozkładem t-Studenta. Ta funkcja jest niezbędna dla każdego, kto chce obliczyć rozkład t-Studenta w Excelu bez skomplikowanych formuł. Jej prawidłowe użycie wymaga zrozumienia trzech kluczowych argumentów.
- x - wartość liczbowa, dla której obliczamy rozkład
- stopnie_swobody - liczba stopni swobody (musi być ≥ 1)
- strony - określa typ rozkładu (1 dla jednostronnego, 2 dla dwustronnego)
Przy korzystaniu z funkcji ROZKŁAD.T należy pamiętać, że liczba stopni swobody musi być większa lub równa 1. Jest to kluczowy warunek poprawności obliczeń.
Dodatkowo, wybór między rozkładem jedno- a dwustronnym zależy od specyfiki badanego problemu i postawionej hipotezy statystycznej. Prawidłowe określenie tego parametru jest kluczowe dla uzyskania wiarygodnych wyników.
Jak wykonać obliczenia krok po kroku?
Obliczanie rozkładu t-Studenta w Excelu może wydawać się skomplikowane, ale można to zrobić w kilku prostych krokach. Oto jak zrobić test t-Studenta w Excelu krok po kroku:
- Otwórz nowy arkusz w Excelu
- Wprowadź wartość t w komórce A1 (np. 1,96)
- W komórce A2 wpisz liczbę stopni swobody (np. 10)
- W komórce A3 wpisz formułę: =ROZKŁAD.T(A1,A2,2) dla rozkładu dwustronnego lub =ROZKŁAD.T(A1,A2,1) dla jednostronnego
- Naciśnij Enter, aby zobaczyć wynik
Te kroki pozwalają szybko i efektywnie obliczyć wartość t-Studenta w Excelu. Pamiętaj, że precyzyjne wprowadzenie danych jest kluczowe dla uzyskania poprawnych wyników.
Przykład praktyczny z konkretnymi danymi
Rozważmy przykład, w którym chcemy sprawdzić, czy średnia waga studentów różni się od 70 kg. Mamy próbę 15 studentów i chcemy przeprowadzić test t-Studenta w Excelu.
| Dane | Wartość |
| Średnia próby | 72.5 kg |
| Odchylenie standardowe próby | 3.2 kg |
| Liczebność próby | 15 |
| Wartość t | 3.046 |
| Stopnie swobody | 14 |
| p-wartość (dwustronna) | 0.0086 |
Wprowadzając te dane do Excela i używając funkcji ROZKŁAD.T, otrzymujemy p-wartość 0.0086. Ta niska wartość sugeruje, że różnica między średnią próby a hipotetyczną średnią populacji jest statystycznie istotna.
Interpretując wyniki, możemy stwierdzić, że istnieją mocne dowody na to, że średnia waga studentów różni się od 70 kg. Excel analiza statystyczna rozkładu t-Studenta pozwala nam wyciągnąć takie wnioski z dużą pewnością statystyczną.
Różnica między rozkładem jednostronnym a dwustronnym
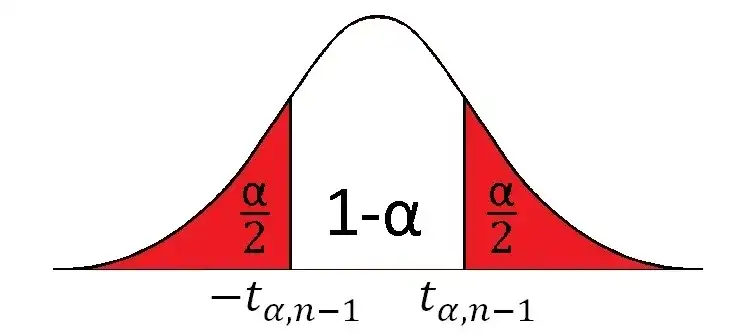
Rozkład jednostronny stosuje się, gdy interesuje nas tylko jeden "ogon" rozkładu. Jest używany, gdy hipoteza alternatywna zakłada, że wartość parametru jest albo większa, albo mniejsza od wartości w hipotezie zerowej.
Rozkład dwustronny bierze pod uwagę oba "ogony" rozkładu. Stosuje się go, gdy hipoteza alternatywna zakłada, że wartość parametru może być zarówno większa, jak i mniejsza od wartości w hipotezie zerowej.
Wybór między rozkładem jedno- a dwustronnym ma kluczowe znaczenie dla interpretacji wyników i wpływa na wartości krytyczne oraz p-wartości w teście t-Studenta w Excelu.
| Typ rozkładu | Zastosowanie |
| Jednostronny | Gdy interesuje nas zmiana w jednym kierunku (np. czy nowa metoda jest lepsza) |
| Dwustronny | Gdy interesuje nas jakakolwiek zmiana (np. czy nowa metoda jest inna) |
Typowe wartości rozkładu t-Studenta
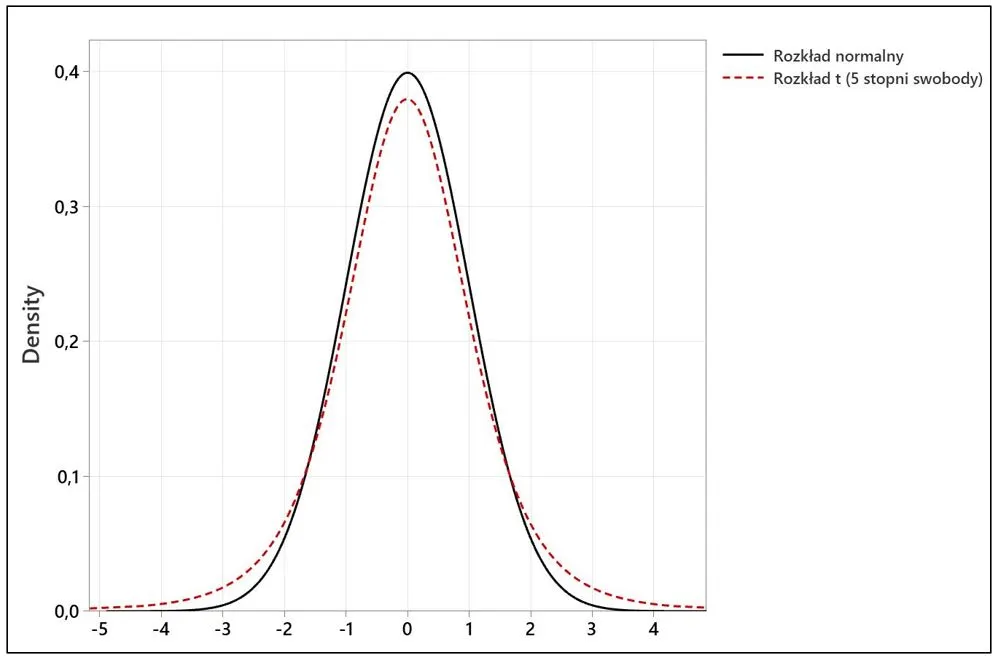
Typowe wartości rozkładu t-Studenta zależą od liczby stopni swobody i poziomu istotności. Dla dużych próbek (powyżej 30) rozkład t-Studenta zbliża się do rozkładu normalnego. Dla mniejszych próbek, rozkład t ma "grubsze ogony", co odzwierciedla większą niepewność wynikającą z mniejszej ilości danych.
Interpretując wyniki, często korzystamy z wartości krytycznych. Na przykład, dla 10 stopni swobody i poziomu istotności 0.05, wartość krytyczna dla testu dwustronnego wynosi około 2.228. Oznacza to, że jeśli obliczona wartość t przekracza 2.228 lub jest mniejsza niż -2.228, odrzucamy hipotezę zerową.
W praktyce, przy obliczaniu wartości t-Studenta Excel jest niezastąpiony. Przykładowo, dla badania efektywności nowej metody nauczania, możemy użyć testu jednostronnego, jeśli spodziewamy się tylko poprawy wyników. Dla badania wpływu zmiany diety na wagę, gdzie waga może zarówno wzrosnąć, jak i spaść, stosujemy test dwustronny.
Zaawansowane funkcje rozkładu t-Studenta
Excel oferuje również bardziej zaawansowane funkcje: ROZKŁAD.T.RT i ROZKŁAD.T.2T. ROZKŁAD.T.RT służy do obliczania prawego ogona rozkładu t-Studenta, co jest szczególnie przydatne w testach jednostronnych. ROZKŁAD.T.2T z kolei oblicza dwustronny rozkład t-Studenta, co upraszcza obliczenia dla testów dwustronnych.
Te funkcje zapewniają większą precyzję obliczeń niż podstawowa funkcja ROZKŁAD.T. Są szczególnie przydatne w zaawansowanych analizach statystycznych, gdzie dokładność jest kluczowa. Ich nazewnictwo jest również bardziej intuicyjne, co ułatwia prawidłowe zastosowanie w różnych scenariuszach badawczych.
Sytuacje wymagające użycia tych zaawansowanych funkcji obejmują skomplikowane analizy danych naukowych, precyzyjne badania medyczne czy zaawansowane analizy finansowe. W takich przypadkach, nawet niewielkie różnice w dokładności obliczeń mogą mieć istotne znaczenie dla końcowych wniosków.
Błędy przy obliczaniu rozkładu t-Studenta
Najczęstsze problemy przy obliczaniu rozkładu t-Studenta w Excelu to nieprawidłowe określenie stopni swobody lub wybór niewłaściwego typu rozkładu (jedno- lub dwustronnego). Te błędy mogą prowadzić do niepoprawnych wniosków statystycznych.
Innym częstym problemem jest nieprawidłowa interpretacja p-wartości lub wartości krytycznych. Może to wynikać z niezrozumienia różnic między testami jedno- i dwustronnymi lub nieuwzględnienia specyfiki badanego problemu.
Aby uniknąć tych błędów, zawsze dokładnie sprawdzaj wprowadzone dane i parametry funkcji. Korzystaj z najnowszych funkcji Excel, takich jak ROZKŁAD.T.RT i ROZKŁAD.T.2T, które oferują większą precyzję. Wreszcie, zawsze interpretuj wyniki w kontekście badanego problemu i pamiętaj o ograniczeniach testu t-Studenta, szczególnie dla małych próbek.
Rozkład t-Studenta w Excelu: Klucz do precyzyjnej analizy statystycznej
Rozkład t-Studenta w Excelu to potężne narzędzie statystyczne, które pozwala na dokładną analizę danych, szczególnie w przypadku małych próbek. Dzięki funkcjom takim jak ROZKŁAD.T, ROZKŁAD.T.RT i ROZKŁAD.T.2T, Excel umożliwia szybkie i precyzyjne obliczenia, które są niezbędne w wielu dziedzinach nauki i biznesu.
Kluczem do skutecznego wykorzystania tego narzędzia jest zrozumienie różnicy między rozkładem jedno- i dwustronnym oraz prawidłowe określenie stopni swobody. Pamiętaj, że test t-Studenta w Excelu krok po kroku wymaga staranności w wprowadzaniu danych i interpretacji wyników. Unikaj typowych błędów, takich jak nieprawidłowy wybór typu rozkładu czy błędna interpretacja p-wartości.
Wykorzystując zaawansowane funkcje i stosując się do przedstawionych wskazówek, możesz z łatwością przeprowadzać analizę statystyczną rozkładu t-Studenta w Excelu. Niezależnie od tego, czy pracujesz nad projektem badawczym, analizujesz dane biznesowe czy prowadzisz kontrolę jakości, rozkład t-Studenta w Excelu stanowi nieocenione wsparcie w podejmowaniu decyzji opartych na solidnych podstawach statystycznych.
